C语言编程：教你如何判断一个数是否为素数

用C语言编写一段程序判断一个整数是否是素数。

这是C编程语言：

#include

intmain(

{

inti,j,k=0;

for(i=2;i<10000>

{

for(j=2;j*j<=i;j++

if(i%j==0)

中断;

{

printf("%d",i);\n");

}

}

}

扩展信息：

这个想法C语言中判断数字一的思路1：判断整数m是否为素数，只要m是2~m-1之间的每一个整数不可整除，m是素数。

此外，如果m不可被任何整数整除，则方法可以更简单。
2到m之间，则m必须是素数。
可以整除，可以确定17是质数

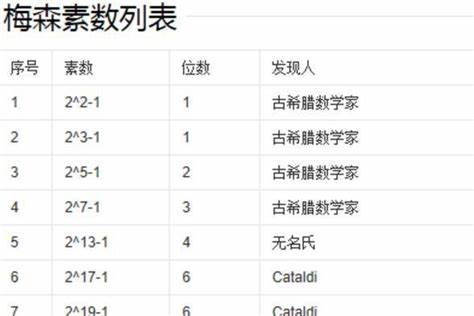
求C语言中判断素数的代码!!!!!

基本思想：用m作为被除数，2-INT()作为除数。
如果两者不可整除，则m为素数，否则不是。

可以用下面的程序段来实现：

voidmain()

{intm,i,k;

printf("请输入数字：\n");

scanf("%d",&m);

k=sqrt(m);

for(i=2;i

if(m%i==0)break;

printf("这个数是素数");

else

printf("这个数不是素数");

else

printf("这个数不是素数");

}

写成函数如果是质数则返回1，否则返回它返回0

intprime(m%)

{inti,k;

k=sqrt(m);

for(i=2;i

if(m%i==0)return0;

return1;

}

扩展信息：

查找目测素数

1基本思想

基本思想使用过滤方法求素数是：

将1开始的正整数在一定范围内从小到大排列，1如果不是素数，则先过滤掉。
从剩余的数中选择最小的质数，然后删除倍数。
依此类推，直到过滤器空了。

如果是：

12345678910

11121314151617181920

21222324252627282930

如果1不是素数，删除它。
剩下的数中，2是最小的，是质数。
如果去掉2的倍数，剩下的数是：

357911131517192123252729

剩下的数是3。
是最小的，是质数去掉3的倍数，以此类推所有数字经过筛选后，质数为发现：

235711317192329

2C++实现

#definerange2000

bool

IsPrime[range+1];

/*set该函数判断i是否为素数。
结果存储在IsPrime[i]DEV中

C++中通过的测试*/

voidset(boolIsPrime[])

{

inti,j;

for(i=0;i<=area;++i)

ISPrime[i]=true;

IsPrime[0]=IsPrime[1]=false;

for(i=2;i<=range;++i)

for(i=2;i<=range;++i)

{

if(

IsPrime[i])

{

for(j=2*i;j<=range;j+=i)

2.

解释：解决这个问题的技巧是如何安排删除的顺序，使得每个非素数只被删除一次。
我在中学时学过一个因子定理。
他说任何非素数都可以分解为素数的连续乘积。

例如16=2^4、18=2*3^2、691488=2^5*3^2*7^4等。
如果分解中最小的素数写在最左边，16=2^4,18=2*9,691488=2^5*21609,;

也就是说，合数N写成N=p^k*q，此时q明显大于p，因为p是因式分解中最小的素数。
由于因式分解的唯一性，将任意合数N写成N=p^k*q的方式也是唯一的。

因为每个非素数只删除一次，所以可以想象这个程序的速度一定相当高。
根据Gries和Misra的文章，线性时间，即与N成正比的时间就足够了（此时我们需要找到2N的质数）。

代码如下：

#include

#include

使用命名空间std;

intmain()

{

intN;

int*Location=newint[N+1];

for(inti=0;i!=N+1;++i)

Location[i]=i;

Location[1]=0//过滤掉部分

intp,q,end;

end=sqrt((double)N)+1;

for(p=2;p!=end;++p)

{

if(位置[p])

{

for(q=p;p*q<=N;++q)

{

for(intk=p*q;k<=N;k*=p)

位置[k]=0;

}

}

}

intm=0;

for(inti=1;i!=N+1;++i)

{

if(位置[i]!=0)

{

cout<<位置[i]<<"";

++m;

}

if(m==0)cout<

}

cout<

返回0;

}

这段代码在VisualStudio2010环境下测试通过。

小数据下，上述两种算法的速度几乎相同。

参考：百度百科-sift法求素数